1- Introducción
1.1- Fundamentos
Los fundamentos de la hidráulica se basan en dos principios fundamentales de la física, a saber:
• Principio de Pascal: el cual expresa que
la presión que ejerce un fluido incompresible y en equilibrio dentro de
un recipiente de paredes indeformables se transmite con igual
intensidad en todas las direcciones y en todos los puntos del fluido.
• Principio de Bernoulli: expone que en un
fluido ideal (sin viscosidad ni rozamiento) en régimen de circulación
por un conducto cerrado, la energía que posee el fluido permanece
constante a lo largo de su recorrido.
La energía de un fluido en cualquier momento
consta de tres componentes: cinética (que es la energía debida a la
velocidad que posee el fluido), potencial o gravitacional (que es la
energía debido a la altitud del fluido), y una energía que podríamos
llamar de "flujo" (que es la energía que un fluido contiene debido a su
presión).
En la siguiente ecuación, conocida como "Ecuación de Bernoulli" expresa matemáticamente este concepto:
v2·ρ
|
|
+ P + ρ·g·z = constante
|
|
2
|
siendo,
v la velocidad del fluido en la sección considerada;
ρ la densidad del fluido;
P es la presión del fluido a lo largo de la línea de flujo;
g la acelaración de la gravedad;
z la altura en la dirección de la gravedad desde una cota de referencia.
Los sistemas hidráulicos, objeto de estudio de este
tutorial, constituyen una de las formas tecnológicas que actualmente
empleamos para la transmisión de potencia en máquinas. Todo sistema
hidráulico está compuesto de los siguientes elementos principales:
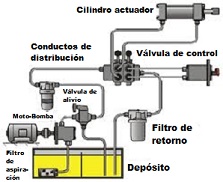
- Un depósito acumulador del fluido hidráulico;
- Una bomba impulsora, que aspirando el fluido desde el depósito crea el flujo en el circuito hidráulico;
- Válvula de control que permite controlar la dirección de movimiento del fluido;
- Actuador o pistón hidráulico, que puede ser de simple o doble efecto, siendo el elemento que transmite la fuerza final;
- Red de conductos por el que circula el fluido desde la bomba hasta los actuadores y retorna al depósito acumulador;
- Filtros de limpieza del fluido hidráulico;
- Válvula de alivio, que proporciona una salida al
sistema en caso de producirse un aumento excesivo de la presión del
fluido dentro del circuito.
1.2- Ventajas e inconvenientes
A continuación se exponen algunas ventajas e
inconvenientes de los sistemas hidráulicos frente a otros sistemas
convencionales de transmisión de potencia:
a) Ventajas:
• Los sistemas hidráulicos permiten desarrollar elevados ratios de fuerza con el empleo de sistemas muy compactos.
• Permiten la regulación continua de las fuerzas que se transmiten, no existiendo riesgo de calentamiento por sobrecargas.
• Son elementos muy flexibles y que pueden
adaptarse a cualquier geometría, gracias a la flexibilidad de los
conductos que conducen el aceite hidráulico hasta los actuadores.
• Los actuadores o cilindros hidráulicos
son elementos reversibles, que pueden actuar en uno u otro sentido y que
además permiten su frenada en marcha. Además son elementos seguros,
haciendo posible su enclavamiento en caso de producirse una avería o
fuga del fluido hidráulico.
b) Inconvenientes:
• La baja velocidad de accionamiento de los actuadores o pistones hidráulicos.
• La alta presión de trabajo exige labores de mantenimiento preventivos (vigilancia de posibles fugas en las juntas).
• Sistema no muy limpio, debido a la presencia de aceites o fluidos hidráulicos.
• En general, es un sistema más caro que otros, por ejemplo los sistemas de aire comprimido.
2- Componentes del sistema
2.1- Fluido hidráulico
Para que un fluido pueda ser empleado como líquido del
circuito de un sistema hidráulico, éste deberá presentar las siguientes
propiedades:
• Ser un fluido incompresible para un rango amplio de presiones;
• Ofrecer una buena capacidad de lubricación en metales y gomas;

• Buena viscosidad con un alto punto de
ebullición y bajo punto de congelación (el rango de trabajo debe oscilar
entre -70ºC hasta +80ºC);
• Presentar un punto de autoignición superior, al menos a los 100ºC;
• No ser inflamable;
• Ser químicamente inerte y no corrosivo;
• Ser un buen disipador de calor, al funcionar también como refrigerante del sistema;
• Presentar buenas condiciones en cuanto a su almacenamiento y manipulación.
Los fluidos hidráulicos presentes en el mercado se pueden agrupar, en general, en tres grandes grupos:
• 1- Fluidos sintéticos de base acuosa: son resistentes a la inflamación. A su vez, se subdividen en dos tipos:
- Emulsiones de agua y aceite. En este tipo de
fluidos, además del aceite de base mineral emulsionable se emplean
aditivos que le confieren propiedades antioxidantes, antidesgaste, etc.
- Soluciones de agua-glicol. Mezclas de 40% glicol y 60% agua, más aditivos especiales.
• 2- Fluidos sintéticos no acuosos: son
compuestos sintéticos orgánicos (fosfatos ésteres simples o clorados,
hidrocarburos clorados y silicatos ésteres). Son caros, pero presentan
un punto de inflamación muy alto.
• 3- Aceites minerales o sintéticos: son
hidrocarburos extraídos del petróleo a los que se le añaden aditivos
químicos, que les confiere unas buenas prestaciones a un coste
relativamente bajo. Son los más usados comercialmente.
La forma de denominar a los fluidos hidráulicos está
regulada según la norma DIN 51524 y 51525. Así, los fluidos hidráulicos
siguiendo esta normativa se denominan todos con la letra H a la
que se le añaden otras letras, para indicar el tipo de aditivos o
propiedades del fluido. A continuación, se muestra la designación de los
fluidos hidráulicos según su tipo:
• Aceites minerales o sintéticos:
- HH: si se trata de un aceite mineral sin aditivos;
- HL: si se trata de un aceite mineral con propiedades antioxidantes y anticorrosivas;
- HP (ó HLP): aceite tipo HL con aditivos que mejoran la resistencia a cargas;
- HM (ó HLM): aceite mineral tipo HL que incluye además aditivos antidesgaste;
- HV: aceite tipo HM que además incorpora aditivos que mejoran su índice de viscosidad.
En ocasiones, a las siglas anteriores se les agrega un
número que indica el coeficiente de viscosidad según DIN 51517
(clasificación de viscosidad según ISO). Ejemplo, HLP 68, que indica:
H: se trata de aceite hidráulico;
L: con aditivos para protección anticorrosivas, con propiedades antioxidantes;
P: posee aditivos que mejora la carga;
68: código de viscosidad, según DIN 51517.
• Fluidos sintéticos de base acuosa:
- HFA: emulsión de aceite en agua (contenido de agua: 80-98%);
- HFB: emulsión de agua en aceite (contenido de agua: 40%);
- HFC: solución de poliglicoles (contenido de agua: 35-55%);
- HFD: líquidos anhídricos (contenido de agua: 0-0,1%).
• Fluidos sintéticos no acuosos:
- HFD-R: aceite a base de esterfosfatos;
- HFD-S: aceite a base de hidrocarburos halogenados;
- HFD-T: aceite a base de mezcla de los anteriores.
Por otro lado, la propiedad que más distingue un
fluido hidráulico de otro es la medida de su viscosidad. La norma DIN
51524 define los siguientes grados para la llamada viscosidad
cinemática, según la tabla siguiente:
ISO
Grados de viscosidad |
Viscosidad cinemática (mm2/s) a 40 ºC
|
|
Mín.
|
Máx.
|
|
ISO VG 10
|
9,0
|
11,0
|
ISO VG 22
|
19,8
|
24,2
|
ISO VG 32
|
28,8
|
35,2
|
ISO VG 46
|
41,4
|
50,6
|
ISO VG 68
|
61,2
|
74,8
|
ISP VG 100
|
90,0
|
110,0
|
Tabla 1. Grados de viscosidad ISO
Decir que la viscosidad cinemática es el cociente
entre la viscosidad absoluta y la densidad del fluido. En el S.I. su
unidad es el m2/s, mientras que en el sistema C.G.S. su unidad es el cm2/s, que se denomina stokes (St).
Por otro lado, la unidad en el S.I. de la viscosidad dinámica o absoluta es el kg/(m·s) ó Pa·s. En el sistema C.G.S., la unidad de la viscosidad absoluta es g/(cm·s), que se denomina poise (P).
La viscosidad del aceite lubricante se expresa con un
número SAE, definido por la Society of Automotive Engineers. Los números
SAE están definidos como: 5W, 10W, 20W, 30W, 40W, etc. En la siguiente
tabla se indica la correlación SAE-ISO:
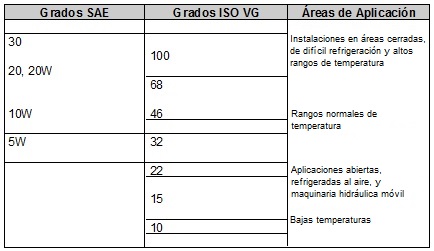
Tabla 2. Correlación entre grados de viscosidad SAE-ISO
Todos los aceites lubricantes se adelgazan cuando su
temperatura aumenta y por el contrario, se espesan cuando su temperatura
disminuye. Si la viscosidad de un aceite lubricante es muy baja, habrá
un excesivo escape por las juntas y los sellos. Si la viscosidad del
aceite lubricante es muy alta, el aceite tiende a "pegarse" y se
necesitará mayor fuerza para bombearlo a través del sistema. Se adjunta
una tabla con los rangos permitidos de viscosidad para los fluidos
hidráulicos.
Viscosidad cinemática (mm2/s)
|
|
Límite inferior
|
10
|
Rango ideal de viscosidad
|
de 15 a 100
|
Límite superior
|
750
|
Tabla 3. Rango de valores de la viscosidad cinemática
2.2- Depósito hidráulico
El depósito o también llamado tanque hidráulico, cumple con varias funciones:
- Además de servir, como uso más inmediato, de
dispositivo por donde se realiza el llenado y vaciado de fluido
hidráulico, sirve también como depósito pulmón desde donde se realiza la
aspiración por parte de la bomba.
- Sirve también como elemento disipador de calor a
través de las paredes del tanque, refrigerando así el aceite contenido
en su interior. Para ello, es necesario que el aceite tenga un tiempo de
residencia mínimo en el interior del tanque de al menos 1 ó 2 minutos.
Así en función del caudal de la bomba, se podría diseñar el volumen del
tanque. En efecto, para una bomba con un caudal de diseño, por ejemplo,
de 10 l/min, haría falta un tanque con capacidad de al menos 20 litros.
- Al servir como depósito de remanso del aceite, se
usa también para la deposición en el fondo de partículas y contaminantes
que se puedan arrastrar del circuito hidráulico, evitándose así que
vuelvan a recircular.
- Además, para aumentar el tiempo de residencia del
aceite en el tanque, se colocan en su interior unos deflectores que
sirven para dirigir la circulación del aceite por el interior del
tanque. Con ello se consigue mayor tiempo de estancia del aceite en el
depósito, y da lugar para que los contaminantes se depositen en el fondo
del tanque, además de favorecer la evaporación del agua que pueda
contener el aceite disuelto y la separación del aire.
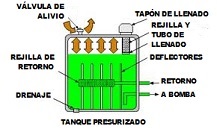
Para un circuito hidráulico se pueden fabricar dos tipos de tanques: presurizados y ventilados.
Los presurizados están sellados, evitándose así que
penetre la suciedad y la humedad en su interior. La presión interna que
se genera a medida que se calienta el fluido hidráulico también sirve
para empujar el aceite hacia la bomba, evitando que se produzca la
cavitación de la misma. No obstante, como medida de seguridad se debe
instalar una válvula hidráulica de alivio, que se utiliza para evitar
que se pueda alcanzar un exceso de presión a medida que el aceite se
calienta, y que pudiera exceder la seguridad del tanque.
Por otro lado, los tanques ventilados, al estar
abiertos a la atmósfera, permiten que haya compensación de presión
cuando se producen cambios en los niveles o en la temperatura del
aceite, y no necesitan de válvula de alivio.
Se adjunta la simbología ISO de los tanques hidráulicos, según el tipo:
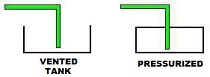
Figura 3. Esquema de representación de un tanque hidráulico
2.3- Filtros
La filtración del fluido hidráulico es necesaria para
evitar que la suciedad producida por el funcionamiento normal del
sistema termine afectando a elementos sensibles de la instalación, como
puedan ser, válvulas o la propia bomba hidráulica.
En la siguiente tabla se recogen los distintos grados de filtración exigidos, según la aplicación del sistema hidráulico.
Grados de Filtración,
en µm |
Tipo de Sistema Hidráulico
|
1-2
|
Para impurezas finas en sistemas altamente sensibles con gran fiabilidad, preferentemente en aviación y laboratorios.
|
2-5
|
Para
sistemas de mando y control sensibles y de alta presión, con
aplicaciones frecuentes en la aviación, robots industriales y máquinas
herramientas.
|
5-10
|
Para sistemas hidráulicos de alta calidad y fiabilidad, con previsible larga vida útil de sus componentes.
|
10-20
|
Para hidráulica general y sistemas hidráulicos móviles, que manejen presiones medianas y tamaños intermedios.
|
15-25
|
Para sistemas de baja presión en la industria pesada o para sistemas de vida útil limitada.
|
20-40
|
Para sistemas de baja presión con holguras grandes.
|
Tabla 4. Grados de filtración y aplicaciones
Cualquier filtro estará compuesto de una carcasa
exterior o envolvente, que contendrá en su interior el material
filtrante. Adicionalmente, dispondrá de una válvula de by-pass, tipo
antirretorno, que se abrirá cuando el material filtrante esté colmado,
de manera que permita un by-pass o paso del flujo del fluido hidráulico
evitando así que el circuito se colpase por culpa del atasco en el
filtro.
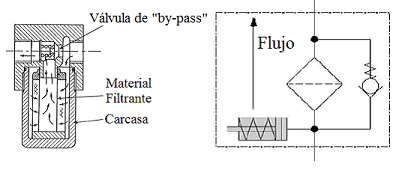
Figura 4. Esquema y símbolo de filtro hidráulico
Un filtro puede ocupar diversas posiciones dentro del
circuito hidráulico, ofreciendo prestaciones muy diversas según se
explica a continuación:
• Filtro situado en la aspiración de la
bomba: es la mejor posición si lo que se pretende es proteger a la
bomba. No obstante, aumenta el riesgo que se produzca cavitación en su
aspiración debido a la pérdida de carga que se origina en el fluido por
su paso por el filtro. Por ello, si se coloca el filtro en esta
posición, éste debe ser de un tipo que ofrezca poca pérdida de carga
localizada, como puedan ser los de tipo de mallas metálicas y los
filtros de superficie con huecos de tamaño grande. Evidentemente, esto
se traduce que el grado de filtración conseguida no sea muy buena. El
tamaño de las partículas filtradas colocando el filtro en esta posición
son relativamente grandes, encontrándose en el rango de los 50 a 100 µm.
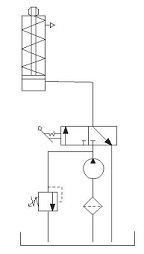
Figura 5. Filtrado en la aspiración
• Filtro situado en el conducto de
impulsión: dada su situación, en la salida de la bomba, se sitúa en la
línea de alta presión. Esto condiciona que los filtros así situados
requieran de una mayor robustez. No obstante, en esta posición se
consiguen filtrados más exigentes, estando el tamaño de las partículas
retenidas en el rango de los 10 a 25 µm.
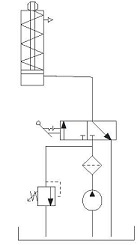
Figura 6. Filtrado en la impulsión
• Filtro en el circuito de retorno al
depósito: a diferencia de los casos anteriores, colocando el filtro en
la tubería de retorno al depósito se evitan los problemas de resistencia
a la presión, o los riesgos de cavitación en la aspiración de la bomba.
Para esta posición, el tamaño de las partículas que se consigue filtrar
se encuentra entre 25 y 30 µm.
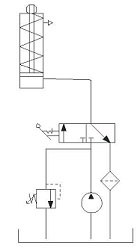
Figura 7. Filtrado en el retorno
• Filtro situado en circuito independiente:
Para circuitos con altas exigencias, el filtro se puede situar en un
circuito independiente que también realice labores de refrigeración del
fluido hidráulico.
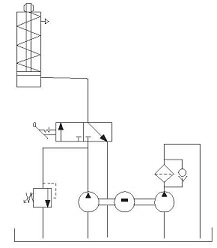
Figura 8. Filtrado en circuito independiente
A continuación se incluye una tabla donde se indican
los grados de filtración y la posición recomendada para situar el
filtro, según el tipo de componente o elemento hidráulico considerado.
Elemento hidráulico
|
Posición recomendada del filtro
|
Grado de filtración,
en µm |
Bomba de émbolos axiales
|
Línea de retorno y/o línea de presión
|
≤ 25
|
Línea de baja presión
|
≤ 25
|
|
Bombas de engranajes y émbolos radiales
|
Línea de retorno
|
≤ 63
|
Válvulas distribuidoras, de presión, de caudal y cierre; cilindros
|
Línea de aspiración
|
≤ 63
|
Motores hidráulicos
|
Línea de retorno
|
≤ 25
|
Tabla 5. Grados de filtración y posiciones del filtro
2.4- Bomba hidráulica
La bomba hidráulica es el componente que genera el
flujo dentro del circuito hidráulico, y está definida por la capacidad
de caudal que es capaz de generar, como ejemplo, galones por minuto,
litros por minuto, o centímetros cúbicos por revolución. Hay dos grandes
grupos de bombas: rotativas y alternativas.
A) Bombas rotativas:
Dentro de la familia de bombas rotativas, se encuentran los siguientes tipos:
• Bombas de engranajes: Las bombas de
engranajes son compactas, relativamente económicas y tienen pocas piezas
móviles, lo que les confiere tener un buen rendimiento.
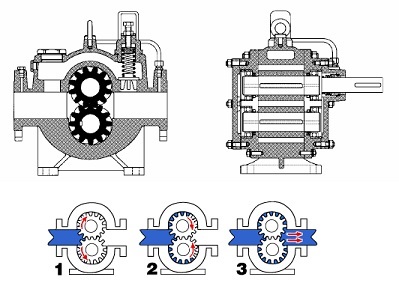
Figura 9. Bomba de engranaje. Principio de funcionamiento
La cilindrada (V) de una bomba de engranaje se obtiene a partir de la siguiente expresión:
π
|
||
V =
|
· (De2 - Di2) · A
|
|
4
|
siendo, De y Di los diámetros de punta y de base del diente del engranaje y A es el ancho de la carcasa de la bomba.
• Bombas lobulares: son bastante semejantes
a las de engranajes, pero con un número de dientes menor y con rangos
de funcionamiento menores. Normalmente se utilizan para incrementos de
presiones bajas donde puede haber problemas de erosión en los dientes si
se empleara una bomba de engranajes.

Figura 10. Bomba hidráulica de tipo lobular
• Bombas de paletas: básicamente constan de
un rotor, paletas deslizantes y una carcasa. Se dividen en dos grandes
tipos, compensadas y no compensadas.
En las bombas de paletas no compensadas cuando el
rotor gira desplaza las paletas hacia fuera debido a la fuerza
centrífuga, haciendo contacto con el anillo, o la carcasa, por lo que se
forma un sello positivo. El fluido en este tipo de bombas entra y va
llenando la porción de volumen mayor que se genera con el hueco dejado
por el rotor descentrado dentro de la carcasa. Al girar entonces se
genera una fuerza que empuja el fluido hacia afuera. Se denominan de
paletas no compensadas porque una mitad del mecanismo de bombeo se
encuentra a una presión inferior a la atmosférica, mientras que la otra
mitad estará sometida a la presión de trabajo propia del sistema.
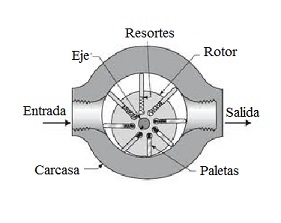
Figura 11. Esquema de una bomba de paletas
Para equilibrar los esfuerzos dentro de la bomba se
desarrollaron las llamadas bombas de paletas compensadas. En este tipo
se cambia la forma circular de la carcasa por otra forma geométrica en
forma de leva, que consigue equilibrar las presiones interiores.
B) Bombas hidráulicas alternativas:
• Bombas de émbolos o pistones: en este
tipo de bombas se convierte el movimiento giratorio de entrada de un eje
en un movimiento de salida axial del pistón. Son un tipo de bombas por
lo general, de construcción muy robustas y adecuadas para presiones y
caudales altos. Su rendimiento volumétrico también es alto.
Se pueden distinguir tres tipos de bombas de pistones:
1. Pistones en línea: tienen una construcción muy simple y el rendimiento que son capaces de obtener puede llegar al 97%.
El cálculo de la cilindrada (V) de una bomba de pistones en línea se obtiene a partir de la siguiente expresión:
π
|
||
V =
|
· D2 · C · Z
|
|
4
|
siendo, C la carrera del pistón, D es el diámetro de cada pistón y Z es el número de pistones.
2. Bombas de pistones radiales: en este tipo se
puede también regular el caudal de cada pistón. Su cilindrada puede ser
fija o variable, y el rendimiento puede llegar a ser de un 99 %.

Bomba de pistones radiales
El cálculo de la cilindrada (V) de una bomba de pistones radiales se obtiene a partir de la siguiente expresión:
π
|
||
V =
|
· e · D2 · Z
|
|
2
|
siendo, e es la excentricidad (o doble de la carrera), D es el diámetro de cada pistón y Z es el número de pistones.
3. Bombas de pistones axiales: también pueden ser de cilindrada fija o variable. En las que son de caudal variable, pueden autorregularse.

Bomba de pistones axiales
La cilindrada (V) de una bomba de pistones axiales se obtiene a partir de la siguiente expresión:
π
|
||
V =
|
· Dp2 · Z · Dm · tgβ
|
|
4
|
siendo, Dp el diámetro de cada pistón, Z es el número de pistones, Dm el diámetro de la máquina y β
es el ángulo de inclinación del eje (que puede ser fijo si la máquina
es de eje recto, o variable si se trata de una máquina con sistema de
inclinación del eje).
• Bombas de diafragma: en este tipo de
bombas el flujo se consigue por el empuje de unas paredes elásticas, de
membrana o diafragma, que varían el volumen de la cámara, aumentándolo y
disminuyéndolo alternativamente.
En la siguiente tabla se resumen los distintos rangos de trabajo de algunos de los tipos de bombas hidráulicas más empleadas:
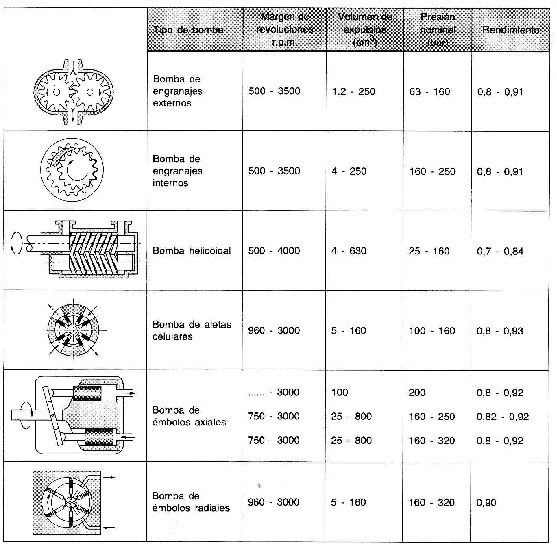
Tabla 6. Rangos de trabajos para las bombas hidráulicas
2.5- Cilindro actuador
El cilindro actuador es el elemento final que
transmite la energía mecánica o empuje a la carga que se desee mover o
desplazar. Aunque hay actuadores de tipo rotativo, los más conocidos son
los cilindros lineales.
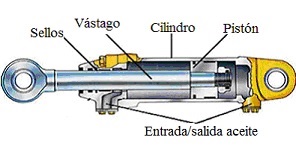
Los cilindros lineales pueden ser de simple o de doble
efecto. En los cilindros de simple efecto el aceite entra sólo por un
lado del émbolo, por lo que sólo puede transmitir esfuerzo en un
sentido. El retroceso se consigue o bien por el peso propio del
cilindro, bien por la acción de un muelle o por una fuerza exterior
(ejemplo, la propia carga que se eleva). Por el contrario, en los
cilindros de doble efecto, el aceite puede entrar por los dos lados del
émbolo, por lo que puede transmitir esfuerzo en los dos sentidos del
movimiento.
Uno de los aspectos a tener en cuenta en el diseño de
un cilindro hidráulico es cómo realizar el amortiguamiento o frenada del
movimiento del vástago, cuando éste se acerca al final de carrera,
evitando así que se produzcan impactos entre el pistón interior y la
tapa del cilindro.
Para ello los cilindros hidráulicos disponen de un
pivote amortiguador que paulatinamente reduce la salida del aceite hasta
que, poco antes de llegar al final de carrera, cierra totalmente el
paso del caudal de salida del aceite, "bypasseando" el flujo mediante
una válvula de estrangulamiento por donde se evacua el resto del aceite.
De este modo se va disminuyendo progresivamente la velocidad del
cilindro y el pistón se consigue frenar suavemente. Este tipo de
amortiguamiento para las posiciones finales de carrera se utiliza si las
velocidades del cilindro oscilan entre 6 m/min y 20 m/min.
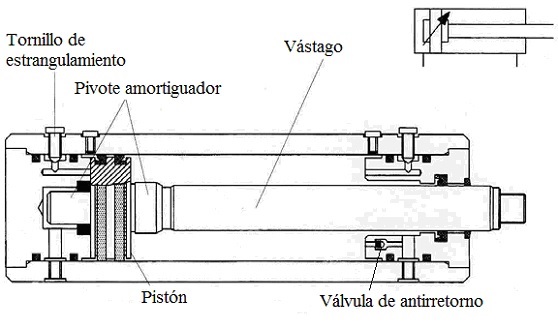
Figura 13. Amortiguamiento del cilindro en final de carrera
Por último, cabe indicar un aspecto a tener muy en
cuenta en el diseño de los cilindros hidráulicos, y en concreto, en lo
que se refiere al vástago.
En efecto, cualquier pieza esbelta sometida a
esfuerzos de compresión, y el vástago estará sometido a este tipo de
solicitación, corre el riesgo de sufrir el fenómeno de pandeo. Para
tener en cuenta este tipo de inestabilidad, el cálculo del diámetro del
vástago se realiza aplicando la Teoría de Euler. Según esta teoría, para
un determinado diámetro (d) de vástago, la fuerza máxima que puede soportar sin que sufra de pandeo viene dada por la siguiente expresión:
K
|
|
F =
|
|
S
|
donde S es un factor de seguridad de valor 3,5 y K es la carga de pandeo (en kg) que se calcula mediante la siguiente expresión:
π2 · E · I
|
|
K =
|
|
L2
|
donde,
E es el módulo de elasticidad, de valor 2,1·106 kg/cm2 para el acero;
I es el momento de inercia de la sección trasversal del vástago, de valor π·d4/64 para un vástago de sección circular de diámetro d;
L es la longitud de pandeo del vástago, que depende del método de sujeción empleado en su montaje.
La longitud de pandeo L, en general no va a
coincidir con la longitud real del vástago, sino que va a depender, como
ya se ha dicho de la forma en que se haya realizado el montaje del
cilindro.
En la siguiente tabla se indica cómo se calcula L en función de las distintas situaciones de montaje del cilindro hidráulico.
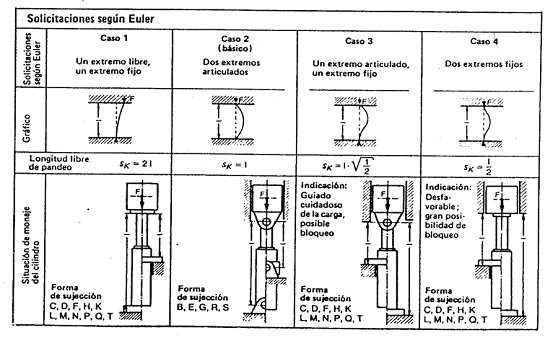
Tabla 7. Cálculo de la longitud libre de pandeo, L
2.6- Tuberías hidráulicas
Para la conducción del fluido hidráulico se emplean
tanto tuberías rígidas de acero sin soldadura, como mangueras flexibles,
evitándose en todo momento emplear elementos galvanizados, dado que el
zinc presente puede ser muy reactivo con ciertos aditivos presentes en
los fluidos hidráulicos.
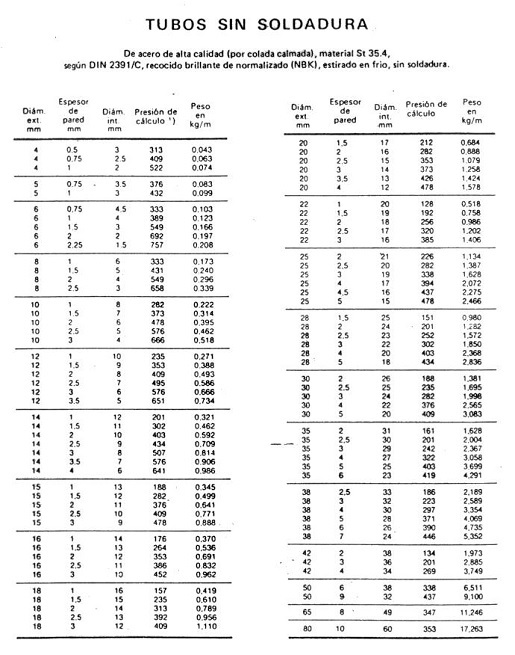
Tabla 8. Tubos de acero sin soldadura para circuitos hidráulicos
Para aplicaciones móviles y de distancias cortas, se suele emplear mangueras flexibles como la que se muestra en la figura.
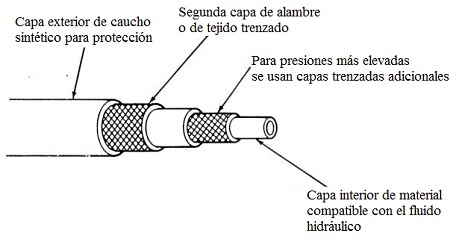
Figura 14. Manguera flexible para aplicaciones hidráulicas
En el caso de mangueras flexibles, en su cálculo hay que tener en cuenta un factor de seguridad Fs, en función de la presión de servicio o de funcionamiento a la que trabaje la manguera.
Factor de Seguridad en mangueras flexibles, Fs
|
|
Presión de servicio, en bares
|
Fs
|
De 0-70
|
8
|
De 70-175
|
6
|
> 175
|
4
|
Tabla 9. Factor de seguridad en mangueras flexibles, Fs
Presión de Rotura
|
|
Fs =
|
|
Presión de Funcionamiento
|
2.7- Válvulas
Las válvulas, como elementos de regulación, de control
y mando de la circulación del fluido hidráulico por el interior del
circuito, pueden ser de diversos tipos: válvulas controladoras de
presión, de caudal, válvulas direccionales o distribuidoras, válvulas de
bloqueo o válvulas de cierre.
• Las válvulas de presión actúan cuando la
presión del fluido en el interior del circuito alcanza un cierto valor,
llamado también valor de tarado.
Según su función las válvulas de presión se clasifican en:
- Válvulas de seguridad: este tipo de válvulas
protegen al circuito de sobrepresiones. Son válvulas normalmente
cerradas, que cuando se alcance una presión límite se activan y
descargan el fluido.
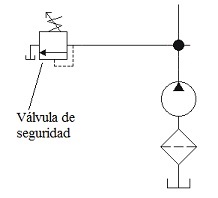
Figura 15. Posición de Válvula de Seguridad
- Válvula de compensación de carga: este tipo de
válvulas se utilizan para mantener una presión mínima aguas arriba,
evitándose así que se pueda producir un fenómeno de embalamiento por
ausencia de una resistencia en el circuito, por ejemplo, en la bajada de
los pistones que elevan la caja de carga de un camión
volquete-basculante.
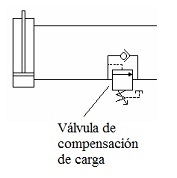
Figura 16. Posición de Válvula de Compensación
• Válvulas de caudal que limitan el caudal
máximo que circula por el circuito, derivando el exceso de caudal al
tanque de retorno.
• Válvulas direccionales que distribuyen el flujo dentro del circuito hidráulico. Las hay de varios tipos:
- Válvulas antirretorno: que permiten el paso del fluido en un sentido y lo impiden en el contrario.
- Válvulas distribuidoras, que pueden ser
correderas o rotativas. En las válvulas correderas las conexiones se
suelen denominar: P, para la línea de presión; T, la de retorno a
tanque; A,B..., las distintas líneas a actuadores, como se muestra en la
figura siguiente.
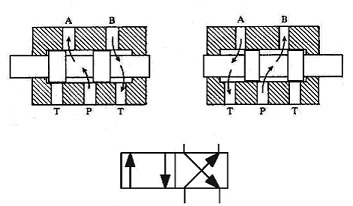
Figura 17. Válvula distribuidora de cuatro vías y dos posiciones
3- Procedimiento de cálculo
3.1- Cálculo del cilindro hidráulico
Conocido el valor de la fuerza de empuje (Fe) o elevación necesaria y el tiempo (t)
disponible en realizar una carrera completa por parte del émbolo, se
emplearían las siguientes expresiones para calcular los parámetros
geométricos que definen al cilindro actuador.
Así, el valor del empuje o fuerza de elevación (Fe) capaz de desarrollar un cilindro hidráulico viene dado por la siguiente expresión:
0,785 · de2 · p
|
|
Fe =
|
|
104
|
siendo,
Fe, el valor de la fuerza desarrollada por el cilindro, en kN.
de, es el diámetro del émbolo que discurre por el interior del cilindro, en mm.
p es la presión de servicio a la que se encuentra el aceite hidráulico en el interior del cilindro, en bar.
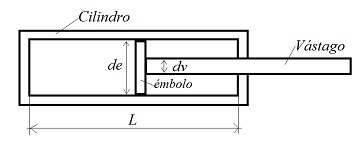
Figura 18. Esquema de un cilindro hidráulico
Para cilindros de doble efecto, durante la carrera de
retroceso o de recogida del émbolo, la fuerza que puede desarrollar
viene calculada por esta otra expresión:
0,785 · (de2 - dv2)· p
|
|
Fr =
|
|
104
|
siendo,
Fr, el valor de la fuerza de retroceso o recogida del émbolo, en kN.
de, es el diámetro del émbolo que discurre por el interior del cilindro, en mm.
dv, es el diámetro exterior del vástago que discurre por el interior del cilindro, en mm.
p es la presión de servicio a la que se encuentra el aceite hidráulico en el interior del cilindro, en bar.
Si se denomina carrera (L) al recorrido completo del émbolo dentro del cilindro, entonces el volumen de una carrera (V), también conocido como cilindrada, viene expresada por el producto de la superficie del émbolo por su carrera, es decir,
π · de2
|
||
V =
|
· L
|
|
4
|
donde,
V, es la cilindrada o volumen de una carrera, en mm3.
de, es el diámetro del émbolo que discurre por el interior del cilindro, en mm.
L, es la longitud de la carrera del vástago, en mm.
Por otro lado, conocida la carrera (L) del vástago y medido el tiempo (t) empleado en su recorrido, se puede calcular la velocidad (v) con que se mueve el vástago, según la expresión siguiente:
L
|
|
v =
|
|
103 · t
|
siendo,
v, la velocidad de salida del vástago, en m/s.
L, es la longitud de la carrera del vástago, en mm.
t, es el tiempo empleado en salir completamente el vástago del cilindro, en segundos (s).
Conocido el volumen de la carrera (V) y el tiempo (t) empleado en la salida del vástago, se puede conocer el caudal (Q) necesario para realizar una carrera, como
60 · V
|
|
Q =
|
|
106 · t
|
donde,
Q, es el caudal de fluido necesario para hacer una carrera, en litros/minuto (l/min).
V, es la cilindrada o volumen de una carrera, en mm3.
t, es el tiempo empleado en salir completamente el vástago del cilindro, en segundos (s).
No obstante, el anterior valor se trata de un valor teórico. El caudal real (Qr)
tenida en cuenta el rendimiento volumétrico del cilindro donde se
reflejan aspectos como la fuga de fluido por las juntas, viene dado por
la siguiente expresión:
Q
|
|
Qr =
|
|
η
|
siendo,
Qr, el caudal real de fluido necesario para hacer una carrera, en litros/minuto (l/min).
Q, es el caudal teórico calculado según la expresión anterior, en litros/minuto (l/min).
η, es el rendimiento volumétrico del cilindro que tiene en cuenta las fugas, como general se toma 0,95.
3.2- Cálculo de las tuberías
Una vez calculado el cilindro actuador y sus
parámetros de diseño (caudal de flujo, geometría), el siguiente paso es
dimensionar los diámetros de los conductos o latiguillos que conducen el
fluido hidráulico hasta los actuadores.
El cálculo del diámetro de los conductos se realiza a partir del caudal (Q) que llega hasta el cilindro actuador, que es un dato conocido y calculado según el apartado anterior.
En efecto, la velocidad del fluido hidráulico (v) por el interior de los conductos está relacionado con el caudal (Q), mediante la siguiente expresión:
Q = v · A
donde
A es el área de la sección interna de la tubería (π · D2 / 4), siendo D el diámetro interior de la tubería.
Por lo tanto, sustituyendo y despejando v de la expresión anterior, el valor de la velocidad (v) del fluido que discurre por el interior de una tubería también puede ser expresada en función del caudal (Q) y del diámetro interior (D) de la tubería, como:
4 · Q
|
|
v =
|
|
π · D2
|
Como norma general, el diámetro (D) de cualquier tubería de conducción de aceite hidráulico se elegirá tal que la velocidad (v)
del fluido por su interior se mantenga dentro de un rango de
velocidades. En la práctica se aplican los siguientes valores estándar
de velocidad en los conductos:
• Tuberías de impulsión:
- hasta 50 bar de presión de trabajo: 4,0 m/s;
- hasta 100 bar de presión de trabajo: 4,5 m/s;
- hasta 150 bar de presión de trabajo: 5,0 m/s;
- hasta 200 bar de presión de trabajo: 5,5 m/s;
- hasta 300 bar de presión de trabajo: 6,0 m/s.
• Tuberías de aspiración: 1,5 m/s;
• Tubería de retorno: 2,0 m/s.
Una vez seleccionado un diámetro (D) para la tubería, se sustituye en la expresión anterior y se recalcula el valor de la velocidad (v)
obtenida, comprobándose que se mantiene dentro del anterior rango
recomendado de velocidades. Es, por tanto, un proceso iterativo.
Una vez seleccionado el diámetro (D) de la tubería y calculada la velocidad (v) de circulación del fluido hidráulico, es necesario conocer la pérdida de carga que se produce por el interior de la tubería.
El cálculo de la pérdida de carga o de presión (Δp)
originado en los tramos de tuberías es inmediato y fácil de realizar.
En efecto, en un tramo de tubería de una longitud considerada "L", el cálculo de las pérdidas de carga originadas se puede obtener aplicando la ecuación de Darcy-Weisbach, mediante la siguiente expresión:
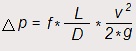
donde,
Δp es el valor de la pérdida de carga o de presión medida según la altura manométrica y expresada en metros de columna de agua (m.c.a.)
L es la longitud del tramo considerado de tubería (m)
D es el diámetro interior de la tubería (m)
v es la velocidad del fluido hidráulico por el interior de la tubería (m/s)
g es la acelaración de la gravedad (9,81 m/s2)
f es el es el factor de fricción de Darcy-Weisbach.
De la anterior expresión todos los parámetros son conocidos salvo el factor de fricción (f).
El factor de fricción (f), es un parámetro adimensional que depende del número de Reynolds (Re) del fluido hidráulico empleado y de la rugosidad relativa de la tubería (εr )
f = f (Re , εr )
donde el número de Reynolds (Re) viene expresado por la siguiente formulación:
Re =
|
ρ · v · D
|
μ
|
siendo,
ρ la densidad del aceite o fluido hidráulico (kg/m3)
v es la velocidad del fluido por el interior de la tubería (m/s)
D es el diámetro interior de la tubería (m)
μ es viscosidad dinámica del aceite o fluido hidráulico (kg/m·s)
Por otro lado, la rugosidad relativa de la tubería (εr ) viene dada en función de la rugosidad absoluta (ε) del material del que está fabricada la tubería y de su diámetro interior (D) de acuerdo a la siguiente expresión:
εr =
|
ε
|
D
|
En la siguiente tabla se muestran los valores de rugosidad absoluta para distintos materiales:
RUGOSIDAD ABSOLUTA DE MATERIALES
|
||||
Material
|
ε (mm)
|
Material
|
ε (mm)
|
|
Plástico (PE, PVC)
|
0,0015
|
Fundición asfaltada
|
0,06-0,18
|
|
Poliéster reforzado con fibra de vidrio
|
0,01
|
Fundición
|
0,12-0,60
|
|
Tubos estirados de acero
|
0,0024
|
Acero comercial y soldado
|
0,03-0,09
|
|
Tubos de latón o cobre
|
0,0015
|
Hierro forjado
|
0,03-0,09
|
|
Fundición revestida de cemento
|
0,0024
|
Hierro galvanizado
|
0,06-0,24
|
|
Fundición con revestimiento bituminoso
|
0,0024
|
Madera
|
0,18-0,90
|
|
Fundición centrifugada
|
0,003
|
Hormigón
|
0,3-3,0
|
|
Tabla 10. Rugosidades absolutas de materiales
El número de Reynolds (Re)
representa la relación entre las fuerzas de inercia y las viscosas en la
tubería. Cuando las fuerzas predominantes son las viscosas (ocurre para
Re con valores bajos), el fluido discurre de forma
laminar por la tubería y la importancia de la rugosidad en la pérdida de
carga es menor que las debida al propio comportamiento viscoso del
fluido. Por otro lado, en régimen turbulento (Re grande), las fuerzas de inercia predominan sobre las viscosas y la influencia de la rugosidad se hace más patente.
Los valores de transición entre régimen laminar y
turbulento se encuentra con el número de Reynolds en la franja de 2000 a
4000. Es decir, en función del valor del número de Reynolds se tiene
que:
• Re < 2000: Régimen laminar.
• 2000 < Re < 4000: Zona crítica o de transición.
• Re > 4000: Régimen turbulento.
Conocer si el flujo que circula por una tubería se
encuentra en el régimen laminar o turbulento es importante porque marca
la manera de calcular el factor de fricción (f).
En efecto, el factor de fricción (f) para
valores del número de Reynolds por debajo del límite turbulento, es
decir, en régimen laminar, se puede calcular aplicando la fórmula de
Poiseuille:
f =
|
64
|
Re
|
expresión que resulta sencilla de aplicar para calcular el factor de fricción (f) conocido el Reynolds (Re).
Para la otra situación, es decir, que nos encontremos
en régimen turbulento, el cálculo para conocer el factor de fricción (f)
ya nos es tan inmediato, y depende tanto del número de Reynolds como de
la rugosidad relativa de la tubería. En este caso existen diversas
formulaciones que pueden ser utilizadas para el cálculo del factor de
fricción:
Y otras como la ecuación de Barr, la ecuación de Miller o la ecuación de Haaland.
No obstante, afortunadamente además de estas
expresiones existen representaciones gráficas y ábacos empíricos que nos
permiten calcular cómodamente el factor de fricción (f). Uno de ellos es el Diagrama de Moody que es la representación gráfica en escala doblemente logarítmica del factor de fricción (f) en función del número de Reynolds (Re) y de la rugosidad relativa de la tubería (ε/D), según se representa en la siguiente figura:
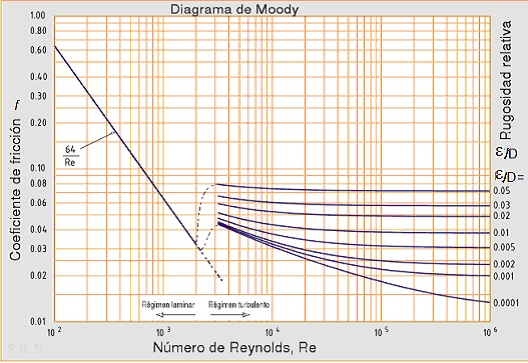
Figura 19. Diagrama de Moody
Por otro lado, para evaluar las pérdidas locales que
se originan en válvulas u otros elementos intercalados en la instalación
(codos, derivaciones en T, bifurcaciones, reducciones...) se pueden
calcular a partir de formulaciones empíricas, como la mostrada en la
expresión siguiente:
Δp = K ·
|
v2
|
2 · g
|
o bien,
Δp = K ·
|
8 · Q2
|
π2 · g · D4
|
donde el coeficiente adimensional K, que mide
la caída de presión se mide experimentalmente y depende del diseño del
fabricante. En la siguiente tabla se dan algunos valores orientativos:
Válvulas (abiertas)
|
Coef. de pérdida, K
|
De bola
|
K = 0,1
|
Compuerta
|
K = 0,1 - 0,3
|
Anti-retorno
|
K = 1,0
|
De asiento estándar. Asiento de fundición
|
K = 4,0 - 10,0
|
De asiento estándar. Asiento de forja (pequeña)
|
K = 5,0 - 13,0
|
De asiento a 45º. Asiento de fundición
|
K = 1,0 - 3,0
|
De asiento en ángulo. Asiento de fundición
|
K = 2,0 - 5,0
|
De asiento en ángulo. Asiento de forja (pequeña)
|
K = 1,5 - 3,0
|
Mariposa
|
K = 0,2 - 1,5
|
Diafragma
|
K = 2,0 - 3,5
|
De macho o tapón. Rectangular
|
K = 0,3 - 0,5
|
De macho o tapón. Circular
|
K = 0,2 - 0,3
|
Otros elementos
|
Coef. de pérdida, K
|
Codos a 90º
|
K = 0,2
|
Derivación
|
K = 0,3
|
Tabla 11. Coeficientes de pérdida de carga, K
Para el cálculo de los coeficientes de pérdidas de
carga en válvulas parcialmente abiertas respecto al valor del
coeficiente en apertura total, se pueden tomar los valores de esta otra
tabla:
Cociente K(parcial)/K(abierta)
|
|||
Situación
|
Compuerta
|
Esfera
|
Mariposa
|
Abierta
|
1,0
|
1,0
|
1,0
|
Cerrada 25%
|
3,0 - 5,0
|
1,5 - 2,0
|
2,0 - 15,0
|
50%
|
12 - 22
|
2,0 - 3,0
|
8 - 60
|
75%
|
70 - 120
|
6,0 - 8,0
|
45 - 340
|
Tabla 12. Coeficientes de pérdida de carga en válvulas parcialmente abiertas
Una vez calculada las pérdidas de cargas localizadas
en cada elemento, codo o válvula del mismo ramal, se suman todas ellas y
se agrega a la pérdida de carga calculada en el tramo recto del tubo,
obteniéndose así la pérdida de carga total por rozamiento en la tubería.
ANEXOS
A.1- Símbolos Hidráulicos

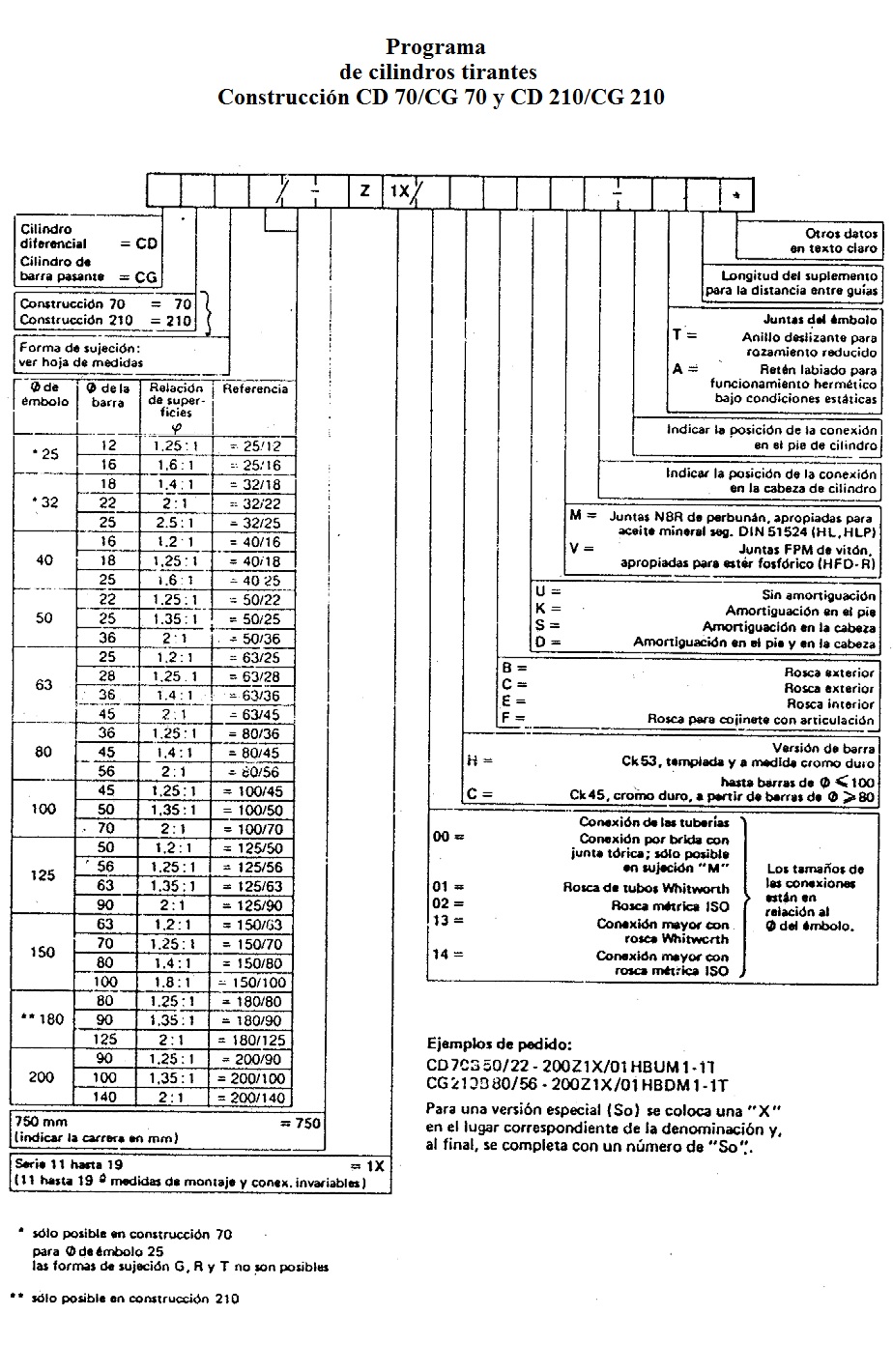
A.2- Codificación de Cilindros Hidráulicos

No hay comentarios:
Publicar un comentario